机器学习一：KNN

KNN（k-nearest neighbor,KNN）算法是最简单也是最重要的机器学习算法之一，它的思想可以用一句话进行概括，即 相似的数据往往拥有相同的类别 。如在常见的花中，十字花科的植物大多数有4片花瓣，而夹竹桃科的植物花瓣大多数是5的倍数。故可以推断同一种类的数据之间的特征更为相似，而不同种类的数据之间的特征差别较大。

下面将具体的介绍KNN算法。

KNN算法的基本原理

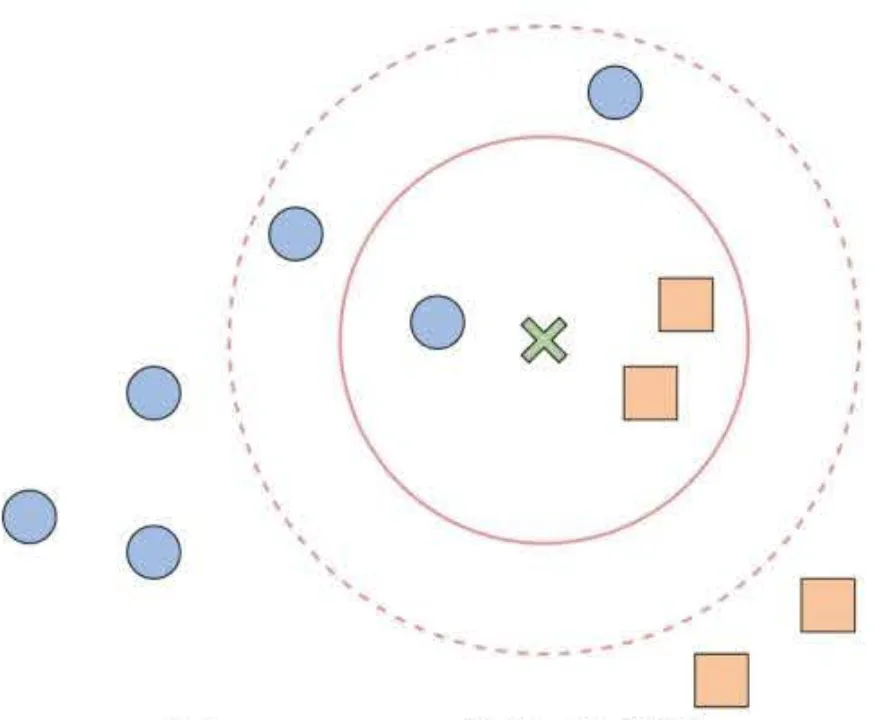
先来看KNN最直观的解释：给定一个训练集，对于新的输入的实例，在训练集中找到与 该实例最近邻的k个实例，这k个实例的多数属于哪个类别，则新输入的实例就属于哪个类别。如下图所示：

其中，新的实例为绿色的X，后续用X来代替，两个已知的类别分为为🔵和🟨 。根据KNN算法的思路：

当k=3时，样本X的3个邻居中有2个🟨和1个🔵，因此将样本X归类为🟨；
当k=5时，样本X的5个邻居中有2个🟨和3个🔵，因此将样本X归类为🔵。

从这个例子中可以看出，KNN的基本思路是让当前样本的分类服从邻居中的多数分类。但是，当K的大小发生变化时，由于邻居的数据变化，其邻居的类别也可能会发现变化，从而改变对当前样本的分类判断。因此，决定K的大小是KNN中最重要的部分之一，K的取值一般是奇数。

当K的取值太小时，分类结果很容易受到分类样本周围的个别噪声数据的影响
当K的取值较大时，分类结果又很有可能将远处一些不相关的样本包含过来

若是想使用比较精确的K值，可以使用K折交叉验证来确定K的大小。

度量距离

如上图的例子所讲，当K=3的时候，我们可以直接肉眼观察出3个邻居中有2个🟨和1个🔵，认为X的类别是🟨。但是计算机无法直接观察出。所以，我们就需要一个度量距离来判断，新输入的类别是输入哪个类别，最常用的度量距离为：

欧式距离

设特征空间 $X$ 是 $n$ 维实数向量空间 $R^n$ ， $x_i,x_j\in X,x_i = (x_i^{(1)},x_i^{(2)},...x_i^{(n)})^T$ ， $x_j = (x_j^{(1)},x_j^{(2)},...x_j^{(n)})^T$ 。

$X_i,X_j的L_p距离可定义为以下的内容:L_p(x_i,x_j) = (\sum_{l=1}^{n}|x_i^{l}-x_j^{l}|^{p})^{\frac{1}{p}}，这里定义p\geq1$

当 $p=1$ 时，称为曼哈顿距离。即： $L_1(x_i,x_j) = (\sum_{l=1}^{n}|x_i^{l}-x_j^{l}|)$
当 $p=2$ 时，称为欧式距离。即： $L_2(x_i,x_j) = (\sum_{l=1}^{n}|x_i^{l}-x_j^{l}|^{2})^{\frac{1}{2}}$
当 $P=\infty$ 时，称为切比雪夫距离（特征差的绝对值的最大值）。即： $L_{\infty}(x_i,x_j) = max_{l}|x_i^{l}-x_j^{l}|$

用以下的例子说明：

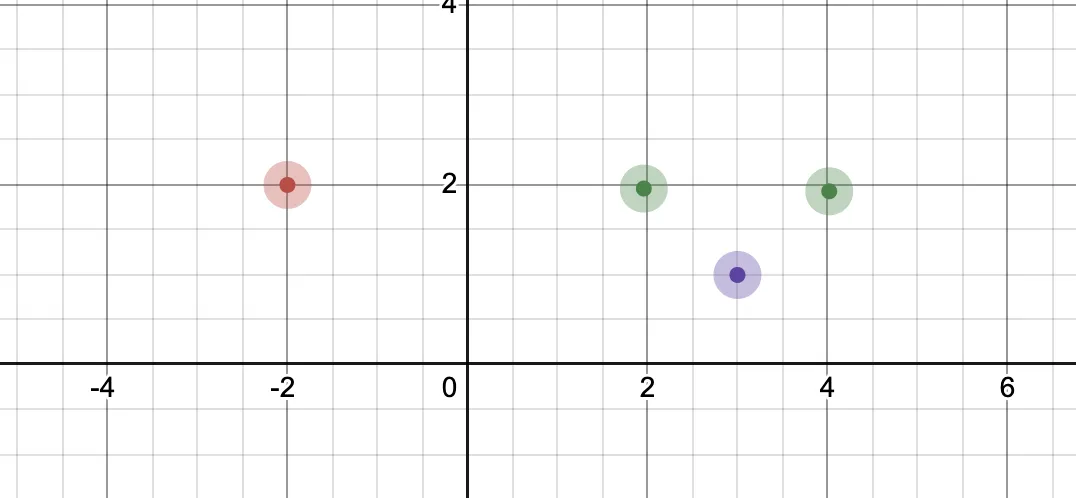
在上图中有两个类，一个是红色的坐标点为(-2,2)，一个是绿色的(2,2)、(4,2)，现在要求紫色的坐标系(3,1)是属于红色类别还是绿色类别，目前的 $k=3$ ，计算如下：

分别计算坐标系(3,1)分别距离两个不同类别的距离：

距离红色的距离: $r = \sqrt{（-2-3）^2+(2-1)^2} = \sqrt{26}$ ；

距离紫色的距离： $p = \sqrt{(2-3)^2+(2-1)^2} + \sqrt{(4-3)^2+(2-1)^2} = 2\sqrt{2}$ .

因为： $2\sqrt{2} < \sqrt{26}$ ，所以认为坐标系(3,1)属于紫色。

sklearn代码

使用的数据集为sklearn自带的iris数据集

import numpy as np
from sklearn.neighbors import KNeighborsClassifier
from sklearn.utils import shuffle
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score

# Load dataset
def get_data():
    data = load_iris()
    x,y = shuffle(data.data, data.target, random_state = 42)
    x = x.astype(np.float32)
    x_trin,x_test,y_train,y_test = train_test_split(x , y, test_size = 0.3, random_state = 42, shuffle = True)
    y_train = y_train.reshape((-1, 1))
    y_test = y_test.reshape((-1, 1))
    return x_trin, y_train, x_test, y_test

下面是训练的过程：

def train_and_evaluate(x_train, y_train, x_test, y_test, n_neighbors=3):
    # Initialize KNN classifier
    knn = KNeighborsClassifier(n_neighbors=n_neighbors)
    
    # Train the model
    knn.fit(x_train, y_train)
    
    # Make predictions
    y_pred = knn.predict(x_test)
    
    # Evaluate accuracy
    accuracy = accuracy_score(y_test, y_pred)
    print(f"Accuracy: {accuracy * 100:.2f}%")

最终的准确率为97.78%。

小结

k 近邻是一种基于距离度量的数据分类模型，其基本做法是首先确定输入实例的 k 个最近邻实例，然后利用这 k 个训练实例的多数所属的类别来预测新的输入实例所属类别。距离度量方式、k 值的选择和分类决策规则是 k 近邻的三大要素。在给定训练数据的情况下，当这三大要素确定时，k 近邻的分类结果就可以确定。常用的距离度量方式为欧式距离，k 作为一个超参数，可以通过交叉验证来获得。

代码链接为：https://github.com/kg5kb8lbj6/happy_machine_learning.git